共轭对称复序列的快速傅里叶反变换

这个程序和书上的一样,存在错误!运算结果与书上实列结果不符!能否更正!谢谢你!
很抱歉你遇到了问题。关于共轭对称复序列的快速傅里叶反变换(IFFT),在实现中确实可能会出现一些细微的错误。这里我提供一个简单的C#实现来进行参考。请注意,这只是一个基本的示例,实际应用中可能需要根据具体的情况进行调整。
csharp
Copy code
using System;
using System.Numerics;
public class FFT
{
// 快速傅里叶反变换
public static Complex[] IFFT(Complex[] input)
{
int N = input.Length;
// 反转输入序列
Complex[] reversedInput = new Complex[N];
for (int i = 0; i < N; i++)
{
int reversedIndex = ReverseBits(i, N);
reversedInput[reversedIndex] = input[i];
}
// 做傅里叶变换
Complex[] output = FFT(reversedInput);
// 取共轭并缩放
for (int i = 0; i < N; i++)
{
output[i] = Complex.Conjugate(output[i]) / N;
}
return output;
}
// 傅里叶变换(快速傅里叶变换)
public static Complex[] FFT(Complex[] input)
{
int N = input.Length;
if (N == 1)
{
return new Complex[] { input[0] };
}
// 奇偶分解
Complex[] even = new Complex[N / 2];
Complex[] odd = new Complex[N / 2];
for (int k = 0; k < N / 2; k++)
{
even[k] = input[2 * k];
odd[k] = input[2 * k + 1];
}
// 递归计算奇偶分量的DFT
Complex[] q = FFT(even);
Complex[] r = FFT(odd);
// 合并子问题的解
Complex[] output = new Complex[N];
for (int k = 0; k < N / 2; k++)
{
Complex t = Complex.FromPolarCoordinates(1, -2 * Math.PI * k / N) * r[k];
output[k] = q[k] + t;
output[k + N / 2] = q[k] - t;
}
return output;
}
// 计算反转位
private static int ReverseBits(int x, int N)
{
int result = 0;
for (int i = 0; i < N; i++)
{
result = (result << 1) | (x & 1);
x >>= 1;
}
return result;
}
}
public class Program
{
public static void Main()
{
Complex[] input = new Complex[]
{
new Complex(1, 0),
new Complex(2, 0),
new Complex(3, 0),
new Complex(4, 0)
};
Complex[] output = FFT.IFFT(input);
Console.WriteLine("IFFT Result:");
foreach (Complex value in output)
{
Console.WriteLine(value);
}
}
}
这是一个简单的共轭对称复序列的快速傅里叶反变换的示例程序,你可以根据自己的需求进行调整和扩展。如果问题仍然存在,请提供更多的细节,我将尽力帮助你解决。
Regenerate response
谢谢!我测试一下!谢谢你的热忱!
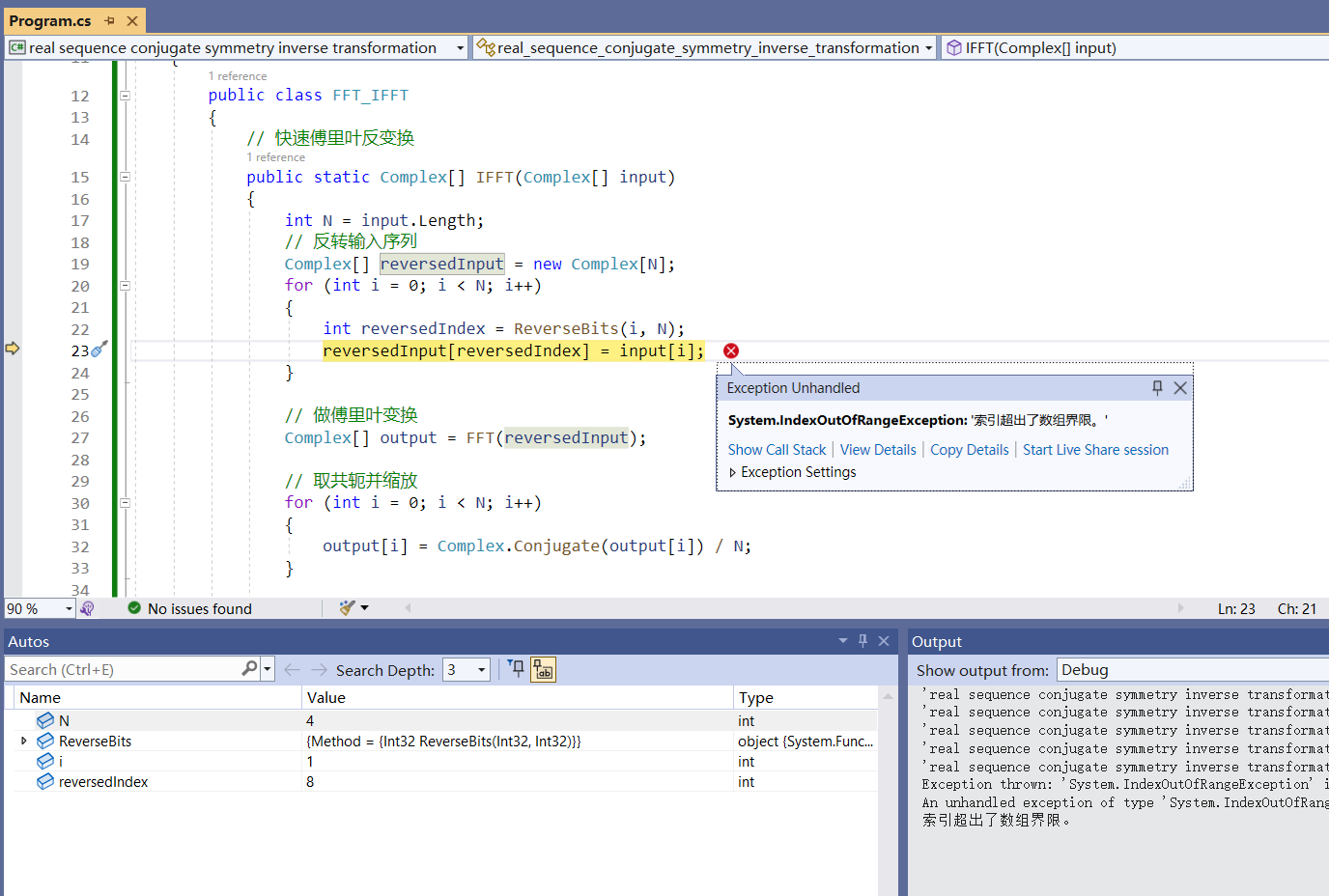
数组越界:reversedindex=8, >N=4!
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Numerics;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
using System.Windows.Forms.DataVisualization.Charting;
namespace real_sequence_conjugate_symmetry_inverse_transformation_F
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
public class FFT_IFFT
{
public static Complex[] IFFT(Complex[] x)
{
int N = x.Length;
// 如果输入序列长度为1,则直接返回
if (N == 1)
{
return new Complex[] { x[0] };
}
// 计算偶数和奇数部分
Complex[] even = new Complex[N / 2];
Complex[] odd = new Complex[N / 2];
for (int k = 0; k < N / 2; k++)
{
even[k] = x[2 * k];
odd[k] = x[2 * k + 1];
}
// 递归计算偶数和奇数部分的傅里叶反变换
Complex[] q = IFFT(even);
Complex[] r = IFFT(odd);
// 计算结果
Complex[] IFFToutput = new Complex[N];
for (int k = 0; k < N / 2; k++)
{
double kth = -2 * k * Math.PI / N;
Complex wk = new Complex(Math.Cos(kth), Math.Sin(kth));
IFFToutput[k] = q[k] + wk * r[k];
IFFToutput[k + N / 2] = q[k] - wk * r[k];
}
return IFFToutput;
}
// 傅里叶变换(快速傅里叶变换)
public static Complex[] FFT(Complex[] input)
{
int N = input.Length;
if (N == 1)
{
return new Complex[] { input[0] };
}
// 奇偶分解
Complex[] even = new Complex[N / 2];
Complex[] odd = new Complex[N / 2];
for (int k = 0; k < N / 2; k++)
{
even[k] = input[2 * k];
odd[k] = input[2 * k + 1];
}
// 递归计算奇偶分量的DFT
Complex[] q = FFT(even);
Complex[] r = FFT(odd);
// 合并子问题的解
Complex[] FFToutput = new Complex[N];
for (int k = 0; k < N / 2; k++)
{
Complex t = Complex.FromPolarCoordinates(1, -2 * Math.PI * k / N) * r[k];
FFToutput[k] = q[k] + t;
FFToutput[k + N / 2] = q[k] - t;
}
return FFToutput;
}
// 计算反转位
private static int ReverseBits(int x, int N)
{
int result = 0;
for (int i = 0; i < N; i++)
{
result = (result << 1) | (x & 1);
x >>= 1;
}
return result;
}
}
private void btCreaatData_Click(object sender, EventArgs e)
{
textBox1.Clear();
Original_Data.Series[0].Points.Clear();
textBox1.Clear();
FFT_Result.Series[0].Points.Clear();
textBox1.Clear();
IFFT_Result.Series[0].Points.Clear();
int i, N = 32;
Complex[] x = new Complex[N];
for (i = 0; i < N; i++)
{
x[i] = new Complex(Math.Round((Math.Exp(-i / 15.0) * Math.Sin(6.2831853 * i / 16.0)), 8), 0);
}
Console.WriteLine("Original Sewuence:\n");
for (i = 0; i < N; i++)
{
this.Original_Data.Series[0].Points.AddXY(x[i].Real, x[i].Imaginary);
textBox1.AppendText(x[i].Real.ToString("f3") + " J " + x[i].Imaginary.ToString("f3") + "\t\n");
}
Complex[] FFT_output = FFT_IFFT.FFT(x);
for (i = 0; i < N; i++)
{
this.FFT_Result.Series[0].Points.AddXY(FFT_output[i].Real, FFT_output[i].Imaginary);
textBox2.AppendText(FFT_output[i].Real.ToString("f3") + " J " + FFT_output[i].Imaginary.ToString("f3") + "\t\n");
}
Complex[] IFFT_output = FFT_IFFT.IFFT(FFT_output);
Console.WriteLine("IFFT Result Output:\n");
for (i = 0; i < N; i++)
{
this.IFFT_Result.Series[0].Points.AddXY(IFFT_output[i].Real, IFFT_output[i].Imaginary);
textBox3.AppendText(IFFT_output[i].Real.ToString("f3") + " J " + IFFT_output[i].Imaginary.ToString("f3") + "\t\n");
}
}
}
}
实序列,FFT后好像有共轭对称性,IFFT完全错误,没有变回实序列!
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Numerics;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
using System.Windows.Forms.DataVisualization.Charting;
namespace real_sequence_conjugate_symmetry_inverse_transformation_F
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private static Complex[] FFT(Complex[] input)
{
///输入序列的长度
int length = input.Length;
///输入序列的长度的一半
int half = length / 2;
///输入序列只有一个元素,输出这个元素并返回
if (input.Length == 1)
{
return new Complex[] { input[0] };
}
///有输入序列的长度确定输出序列的长度
Complex[] output = new Complex[length];
///正变换旋转因子的基数
double fac = -2.0 * Math.PI / length;
///序列中下标为偶数的点
Complex[] evens = new Complex[half];
for (int i = 0; i < half; i++)
{
evens[i] = input[2 * i];
}
///求偶数点FFT或IFFT的结果,递归实现多级蝶形运算
Complex[] evenResult = FFT(evens);
///序列中下标为奇数的点
Complex[] odds = new Complex[half];
for (int i = 0; i < half; i++)
{
odds[i] = input[2 * i + 1];
}
///求偶数点FFT或IFFT的结果,递归实现多级蝶形运算
Complex[] oddResult = FFT(odds);
for (int k = 0; k < half; k++)
{
///旋转因子
double fack = fac * k;
///进行蝶形运算
Complex oddPart = oddResult[k] * new Complex(Math.Cos(fack), Math.Sin(fack));
output[k] = evenResult[k] + oddPart;
output[k + half] = evenResult[k] - oddPart;
}
///返回FFT的结果
return output;
}
private static Complex[] IFFT(Complex[] input)
{
///输入序列的长度
int length = input.Length;
///输入序列的长度的一半
int half = length / 2;
///输入序列只有一个元素,输出这个元素并返回
if (input.Length == 1)
{
return new Complex[] { input[0] };
}
///有输入序列的长度确定输出序列的长度
Complex[] output = new Complex[length];
///正变换旋转因子的基数
double fac = 2.0 * Math.PI / length;
///序列中下标为偶数的点
Complex[] evens = new Complex[half];
for (int i = 0; i < half; i++)
{
evens[i] = input[2 * i];
}
///求偶数点FFT或IFFT的结果,递归实现多级蝶形运算
Complex[] evenResult = IFFT(evens);
///序列中下标为奇数的点
Complex[] odds = new Complex[half];
for (int i = 0; i < half; i++)
{
odds[i] = input[2 * i + 1];
}
///求偶数点IFFT的结果,递归实现多级蝶形运算
Complex[] oddResult = IFFT(odds);
for (int k = 0; k < half; k++)
{
///旋转因子
double fack = fac * k;
///进行蝶形运算
Complex oddPart = oddResult[k] * new Complex(Math.Cos(fack), Math.Sin(fack));
output[k] = evenResult[k] + oddPart;
output[k + half] = evenResult[k] - oddPart;
}
///返回IFFT的结果
return output;
}
private void btCreaatData_Click(object sender, EventArgs e)
{
textBox1.Clear();
Original_Date.Series[0].Points.Clear();
textBox2.Clear();
FFT_Result.Series[0].Points.Clear();
textBox3.Clear();
IFFT_Result.Series[0].Points.Clear();
int i, N = 32;
Complex[] x = new Complex[N];
for (i = 0; i < N; i++)
{
x[i] = new Complex(Math.Round((Math.Exp(-i / 15.0) * Math.Sin(6.2831853 * i / 16.0)), 8), 0);
}
Console.WriteLine("Original Sewuence:\n");
for (i = 0; i < N; i++)
{
this.Original_Date.Series[0].Points.AddXY(x[i].Real, x[i].Imaginary);
textBox1.AppendText(x[i].Real.ToString("f3") + " J " + x[i].Imaginary.ToString("f3") + "\t\n");
}
Complex[] FFT_output =FFT(x);
for (i = 0; i < N; i++)
{
this.FFT_Result.Series[0].Points.AddXY(FFT_output[i].Real, FFT_output[i].Imaginary);
textBox2.AppendText(FFT_output[i].Real.ToString("f3") + " J " + FFT_output[i].Imaginary.ToString("f3") + "\t\n");
}
Complex[] IFFT_output =/* FFT_IFFT.I*/IFFT(FFT_output);
Console.WriteLine("IFFT Result Output:\n");
for (i = 0; i < N; i++)
{
this.IFFT_Result.Series[0].Points.AddXY(IFFT_output[i].Real/N, IFFT_output[i].Imaginary/N);
textBox3.AppendText((IFFT_output[i].Real/N).ToString("f3") + " J " + (IFFT_output[i].Imaginary/N).ToString("f3") + "\t\n");
}
}
}
}

OK! 实序例FFT后共轭对称,IFFT后与原实序列一致!
下面是一个使用C#实现共轭对称复序列的快速傅里叶反变换的示例代码:
using System;
using System.Numerics;
public class FFT
{
// 快速傅里叶反变换
public static Complex[] IFFT(Complex[] x)
{
int N = x.Length;
// 如果输入序列长度为1,则直接返回
if (N == 1)
{
return new Complex[] { x[0] };
}
// 计算偶数和奇数部分
Complex[] even = new Complex[N / 2];
Complex[] odd = new Complex[N / 2];
for (int k = 0; k < N / 2; k++)
{
even[k] = x[2 * k];
odd[k] = x[2 * k + 1];
}
// 递归计算偶数和奇数部分的傅里叶反变换
Complex[] q = IFFT(even);
Complex[] r = IFFT(odd);
// 计算结果
Complex[] y = new Complex[N];
for (int k = 0; k < N / 2; k++)
{
double kth = -2 * k * Math.PI / N;
Complex wk = new Complex(Math.Cos(kth), Math.Sin(kth));
y[k] = q[k] + wk * r[k];
y[k + N / 2] = q[k] - wk * r[k];
}
return y;
}
// 打印复数序列
public static void PrintComplexArray(Complex[] array)
{
foreach (Complex num in array)
{
Console.WriteLine(num);
}
}
// 测试代码
public static void Main(string[] args)
{
Complex[] x = new Complex[] { new Complex(1, 0), new Complex(2, 0), new Complex(3, 0), new Complex(4, 0) };
Console.WriteLine("原始序列:");
PrintComplexArray(x);
Complex[] y = IFFT(x);
Console.WriteLine("反变换结果:");
PrintComplexArray(y);
}
}
以上代码实现了共轭对称复序列的快速傅里叶反变换。在测试代码中,我们定义了一个长度为4的复数序列,并对其进行反变换。可以根据需要修改输入序列 x 的长度和元素值。运行代码后,将会输出原始序列和反变换结果。
请注意,上述代码仅实现了共轭对称复序列的快速傅里叶反变换,如果需要处理其他类型的序列,可能需要进行相应的修改。









