求一段C++代码优化(关于39665条向量求内积的)
0

主要做的就是39665条数据,每条数据是一个向量,根据Pearson公式,求出任意两个数据之间的相关度,即有39665 * 39664 /2 = 782318790条数据,粗略的就需要这么多次运算。每个向量是一个1 * 5的向量,下面是我自己写的代码,大家看下怎么优化一下,不然太慢了。(之前数据是6217时,最后运行的时间是10分钟左右,换成39665后,这都已经快2小时了,还没动静)
补充:
Pearson公式如下:
@M2714E1`9OHEB.jpg)

我这里给的数据已经是每一个向量X - X的平均值了,方便了计算,和节约时间。也就是程序里面只需要计算两两向量之间的内积,然后除以他们的模的成绩。即代码的84 85两行
下面是我的代码,哪位要是matlab写的好的,能帮忙写一份matlab代码也更好了。
后面也列了下之前写的matlab程序,但自己不熟悉matlab,所以那个代码存在很多重复计算问题
1 // CalculatePearsonCorrelation.cpp : 定义控制台应用程序的入口点。 2 // 3 4 #include "stdafx.h" 5 #include <iostream> 6 #include <fstream> 7 #include <sstream> 8 #include <string> 9 #include <algorithm> 10 #include <numeric> //inner_product 11 #include <vector> 12 #include<windows.h> //计算时间 13 #include <iterator> 14 15 using namespace std; 16 17 struct network 18 { 19 int vertexI; 20 int vertexJ; 21 double Cij; 22 }; // 由于最后输出到文件的是: 顶点1编号 顶点2编号 相关系数,所以这里定义一个结构体 23 24 // 读取原始39665数据的函数 25 void readFileToVector(const string& fileName, vector<vector<double> >& sourceMeanData) 26 { 27 DWORD start = GetTickCount(); 28 29 sourceMeanData.clear(); 30 31 ifstream infile(fileName.c_str()); 32 string line; 33 while (getline(infile,line)) 34 { 35 vector<double> vecTmp; 36 vecTmp.clear(); 37 istringstream stream(line); 38 double inputValTmp; 39 while (stream >> inputValTmp) 40 { 41 vecTmp.push_back(inputValTmp); 42 } 43 sourceMeanData.push_back(vecTmp); 44 } 45 infile.close(); 46 47 printf("readFileToVector %ds\n", (GetTickCount()-start)/1000); 48 } 49 50 // 计算39665数据中每一个的模,把结果先保存下来,不然后边每次算任意两个之间的Pearson时,都还得重新算,浪费时间 51 void calculateVectorModel(vector<vector<double> >& sourceMeanData, vector<double>& InnerProductData) 52 { 53 DWORD start = GetTickCount(); 54 55 InnerProductData.clear(); 56 57 double product = 0.0; 58 vector<vector<double> >::const_iterator iter = sourceMeanData.begin(); 59 for (; iter != sourceMeanData.end(); ++iter) 60 { 61 product = 0.0; 62 product = inner_product(iter->begin(), iter->end(), iter->begin(), 0.0); 63 InnerProductData.push_back(sqrt(product)); 64 } 65 66 printf("calculateVectorModel %ds\n", (GetTickCount()-start)/1000); 67 } 68 69 // 最重要的函数,计算符合条件(Cij >= 0.96)的数据 70 void handleFile(vector<vector<double> >& sourceMeanData, vector<double>& InnerProductData, vector<network>& matchConditionData) 71 { 72 DWORD start = GetTickCount(); 73 // 处理数据 74 vector<vector<double> >::iterator iter1 = sourceMeanData.begin(); 75 vector<vector<double> >::iterator iter2 = iter1; 76 double product = 0.0; 77 int idxI = 1; 78 int idxJ = 1; 79 for (; iter1 != sourceMeanData.end(); ++iter1, ++idxI) 80 { 81 for (iter2 = iter1 + 1, idxJ = idxI + 1; iter2 != sourceMeanData.end(); ++iter2, ++idxJ) 82 { 83 product = 0.0; 84 product = inner_product(iter1->begin(), iter1->end(), iter2->begin(), 0.0); 85 double Cij = product / (InnerProductData[idxI-1] * InnerProductData[idxJ-1]); 86 if (abs(Cij) >= 0.96) 87 { 88 network networkTmp; 89 networkTmp.vertexI = idxI; 90 networkTmp.vertexJ = idxJ; 91 networkTmp.Cij = Cij; 92 matchConditionData.push_back(networkTmp); 93 } 94 } 95 } 96 97 printf("handleFileData %ds\n", (GetTickCount()-start)/1000); 98 99 } 100 101 // 符合条件的数据写入磁盘文件 102 void writeFileToDisk(const string& fileName, vector<network>& matchConditionData) 103 { 104 DWORD start = GetTickCount(); 105 106 ofstream outfile(fileName.c_str()); 107 vector<network>::iterator iter = matchConditionData.begin(); 108 for (; iter != matchConditionData.end(); ++iter) 109 { 110 outfile << iter->vertexI << '\t' << iter->vertexJ << '\t' << iter->Cij << endl; 111 } 112 113 printf("writeFileToDisk %ds\n", (GetTickCount()-start)/1000); 114 115 } 116 117 int _tmain(int argc, _TCHAR* argv[]) 118 { 119 DWORD start = GetTickCount(); 120 121 // 三个要一直用的数据向量:均值向量、内积向量、符合Pearson条件的结果向量 122 vector<vector<double> > meanData; 123 meanData.clear(); 124 vector<double> InnerProductData; 125 InnerProductData.clear(); 126 vector<network> matchConditionData; 127 matchConditionData.clear(); 128 129 130 131 132 // 测试程序是否正确的小规模数据集以及测试过程 133 string filenametmp = "E://VsProg//数据处理文件夹//20120428//处理后数据集//GSE10785_matrix//VectorXsubVectorXMean//MeanAdiposeB6_lean4wk.txt"; 134 string fileOuttmp = "E://VsProg//数据处理文件夹//20120428//处理后数据集//GSE10785_matrix//NetWork.txt"; 135 readFileToVector(filenametmp, meanData); 136 calculateVectorModel(meanData, InnerProductData); 137 handleFile(meanData, InnerProductData, matchConditionData); 138 writeFileToDisk(fileOuttmp, matchConditionData); 139 140 141 142 143 printf("AllTime %ds\n", (GetTickCount()-start)/1000); 144 145 return 0; 146 }
下面给列一些原始数据,方便形象理解代码。
// 我这里列了10个,其中每个向量是 1 * 5 -0.08686 -0.02222 0.02571 -0.0108 0.09417 -0.055414 0.043566 0.009326 -0.059304 0.061826 0.014422 0.020222 0.014862 -0.006678 -0.042828 -0.104204 0.060776 0.196706 -0.013234 -0.140044 -0.06272 0.1319 0.06158 -0.02788 -0.10288 0.096898 0.082048 0.027678 -0.060092 -0.146532 -0.094522 -0.021122 0.211278 -0.040412 -0.055222 0.043442 0.018842 -0.005408 -0.120628 0.063752 0.025998 -0.085142 0.037948 -0.046442 0.067638 0.005396 0.012666 -0.065774 0.013446 0.034266
matlab代码
1 expData = importdata("E://VsProg//数据处理文件夹//20120428//处理后数据集//GSE10785_matrix//VectorXsubVectorXMean//MeanAdiposeB6_lean4wk.txt"); 2 fid = fopen("E://VsProg//数据处理文件夹//20120428//处理后数据集//GSE10785_matrix//NetWork.txt", 'w+'); 3 length = size(expData, 1); 4 width = size(expData, 2); 5 avg = zeros(length,1); 6 for k = 1 : length 7 avg(k) = mean(expData(k, 2 : width)); 8 end 9 10 for i = 1 : length 11 lineI = expData(i, 2 : width) - avg(i); 12 for j = i + 1 : length 13 lineJ = expData(j, 2 : width) - avg(j); 14 fenzi = dot(lineI,lineJ); 15 fenmu = (dot(lineI,lineI) * dot(lineJ,lineJ)) ^ (1/2); 16 Cij = fenzi / fenmu; 17 if abs(Cij) >= 0.98 18 fprintf(fid, '%d\t%d\t%f\n', i, j, Cij); 19 end; 20 end; 21 end;
先谢谢大家了~~
最佳答案
0

用这个式子进行计算会不会更好点呢?
收获园豆:20
看不到图?
@ziyoudefeng:  额 现在呢
额 现在呢
@ziyoudefeng: 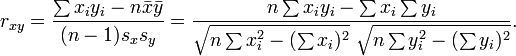 now?
now?
@grass of moon:
谢谢你~不过感觉问题不在公式上,我在这里计算之前已经是求的向量减去他们的平均值之后的值了。不管什么公式,总的计算次数都是( n * (n-1) ) / 2。
最近不处理这个工作了,如果再用的话,想着能不能试试多线程。
谢谢你的回答。
@ziyoudefeng: 其实如果能跑GPU的话,可以直接用CUDA编写实现并行计算的,那样应该会快很多










