一道算法题，提供思路都给分
0
悬赏园豆：200
[已解决问题]
解决于 2011-12-10 19:10
有一个采购经理，需要去4个工厂采供钢材，这里4个工厂分别为工厂A，工厂B，工厂C，工厂D。钢材的类型有1,2,3,4,5,6...10000种。
由于这个经理和这些工厂都认识，彼此有交情，所以当要采购100吨钢材的时候，他会将40顿钢材分配给工厂A，30吨钢材分配给工厂B，20吨钢材分配给工厂C，10吨钢材分配给工厂D。
同一种钢材只能在同一个工厂中采集，每一种要采集的钢材都有一个采集量：例如m1,m2,m3...m10000,
这里m1代表采购第一种钢材m1吨
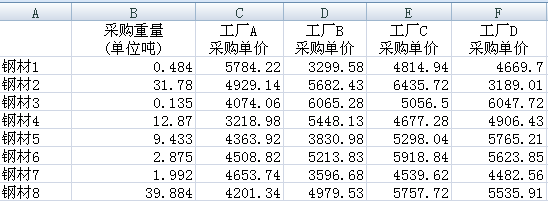
每一种钢材在每个工厂中的价格都不一样，例如
ma1,mb1,mc1,md1.
ma1:第一种钢材在a工厂的单价
mb2:第二种钢材在b工厂的单价
话的总钱=m1*mX1+m2*mX2...m10000*mX10000
X:代表在那个工厂采购的价格。
求满足采购要求的方案，此方案下采购经理花的钱最少。
最佳答案
0
这道题看起来不难，但是做起了很烦。
我大一的时候学运筹学，在单纯形法那里都是这种题。
不过现在不接触运筹学久矣。
过程很复杂，建议你找一本运筹学的（电子）书了解一下。
运筹学开篇就是单纯形法，所以是二维解法中最简单的。
收获园豆：100
的确，已经用遗传算法解决了
其他回答(6)
0
太好了， 看来又是一个不错的问题， 我去算算然后给你答案。
收获园豆：10
0
这个是比较简单的先行规划问题。高中数学的知识就能搞定。回去自己找高中的先行规划知识，然后把求出的结果表达式用程序来计算就ok了
收获园豆：10
有10000种钢材，数据量很大.线性规划很难算出来。
0
我可以回去想想，看看能解决不。不知道这个题，对四个厂家订货分配是不是按百分比。
当要采购100吨钢材的时候，他会将40顿钢材分配给工厂A，30吨钢材分配给工厂B，20吨钢材分配给工厂C，10吨钢材分配给工厂D。
这是不是说按40%给A，30%给B，。。。
收获园豆：10
是的，因为不可能完美的匹配到40%，30% 所以允许有上下5%的浮动.
0
感觉每种钢材先找出价格最低的厂家，然后看看有无落选的厂家，如果有，找出这些厂家价格与最低价的差值，然后找差值最小的。感觉这个属于一个运筹学里面的经典问题，只是厂家多了，不好手工计算。。。
收获园豆：10
0
遗传算法
收获园豆：50
0
同一种只能在同一个厂采购，那么他怎么分给其他3个厂呢？
然后是不是分配都是固定的，也就是a 40， b30， c20， d10这种？如果都是固定的，那么究竟题目要求规划什么？
收获园豆：10
