急急急!!!!有谁懂多元线性回归的?
此问题本人已经自己解决,下面的是具体实现,最后一个方法getparams()就是最后的求多元线性方程的各参数组成的数组,本人已亲测,安全无痛,有需要的拿走,不谢。
public function get_complement($data, $i, $j)
{
/* x和y为矩阵data的行数和列数 */
$x = count($data);
$y = count($data[0]);
/* data2为所求剩余矩阵 */
$data2 = [];
for ($k = 0; $k < $x - 1; $k ++) {
if ($k < $i) {
for ($kk = 0; $kk < $y - 1; $kk ++) {
if ($kk < $j) {
$data2[$k][$kk] = $data[$k][$kk];
} else {
$data2[$k][$kk] = $data[$k][$kk + 1];
}
}
} else {
for ($kk = 0; $kk < $y - 1; $kk ++) {
if ($kk < $j) {
$data2[$k][$kk] = $data[$k + 1][$kk];
} else {
$data2[$k][$kk] = $data[$k + 1][$kk + 1];
}
}
}
}
return $data2;
}
/* 计算矩阵行列式 */
public function cal_det($data)
{
$ans = 0;
if (count($data[0]) === 2) {
$ans = $data[0][0] * $data[1][1] - $data[0][1] * $data[1][0];
} else {
for ($i = 0; $i < count($data[0]); $i ++) {
$data_temp = $this->get_complement($data, 0, $i);
if ($i % 2 === 0) {
$ans = $ans + $data[0][$i] * ($this->cal_det($data_temp));
} else {
$ans = $ans - $data[0][$i] * ($this->cal_det($data_temp));
}
}
}
return $ans;
}
/*计算矩阵的伴随矩阵*/
public function ajoint($data)
{
$m = count($data);
$n = count($data[0]);
$data2 = [];
for ($i = 0; $i < $m; $i ++) {
for ($j = 0; $j < $n; $j ++) {
if (($i + $j) % 2 === 0) {
$data2[$i][$j] = $this->cal_det($this->get_complement($data, $i, $j));
} else {
$data2[$i][$j] = -$this->cal_det($this->get_complement($data, $i, $j));
}
}
}
return $this->trans($data2);
}
/*转置矩阵*/
public function trans($data)
{
$i = count($data);
$j = count($data[0]);
$data2 = [];
for ($k2 = 0; $k2 < $j; $k2 ++) {
for ($k1 = 0; $k1 < $i; $k1 ++) {
$data2[$k2][$k1] = $data[$k1][$k2];
}
}
/*将矩阵转置便可得到伴随矩阵*/
return $data2;
}
/*求矩阵的逆,输入参数为原矩阵*/
public function inv($data)
{
$m = count($data);
$n = count($data[0]);
$data2 = [];
$det_val = $this->cal_det($data);
$data2 = $this->ajoint($data);
for ($i = 0; $i < $m; $i ++) {
for ($j = 0; $j < $n; $j ++) {
$data2[$i][$j] = $data2[$i][$j] / $det_val;
}
}
return $data2;
}
/*求两矩阵的乘积*/
public function getProduct($data1, $data2)
{
/*$data1 为左乘矩阵*/
$m1 = count($data1);
$n1 = count($data1[0]);
$m2 = count($data2);
$n2 = count($data2[0]);
$data_new = [];
if ($n1 !== $m2) {
return false;
} else {
for ($i = 0; $i <= $m1 -1; $i ++) {
for ($k = 0; $k <= $n2 - 1; $k ++) {
$data_new[$i][$k] = 0;
for ($j = 0; $j <= $n1 - 1; $j ++) {
$data_new[$i][$k] += $data1[$i][$j] * $data2[$j][$k];
}
}
}
}
return $data_new;
}
/*多元线性方程*/
public function getParams($arr_x, $arr_y)
{
$final = [];
$arr_x_t = $this->trans($arr_x);
$result = $this->getProduct($this->getProduct($this->inv($this->getProduct($arr_x_t, $arr_x)), $arr_x_t), $arr_y);
foreach ($result as $key => $val) {
foreach ($val as $_k => $_v) {
$final[] = $_v;
}
}
return $final;
}
不知道你说的是懂还是精通,
如果是懂的话, 那算我一个吧!
需求是这样的
根据 类似$arr_x = [[1, 5, 10], [1, 10, 20], [1, 20, 40]]的二维数组,你可以把他想象成一个矩阵, $arr_y = [5, 10, 15] 这个也是可以想象成一个矩阵,然后根据 $arr_x 和$arr_y拟合出一个多元的线性方程,公式是这样的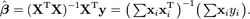
@清华大学副院长: 抱歉, 我级别不够。
@请叫我头头哥: 那这么和你说吧,求一个矩阵的逆矩阵你会吧?就是根据伴随矩阵求逆矩阵,然后写一个方法,传入一个矩阵,也就是二维数组,然后返回这个矩阵的逆矩阵
@请叫我头头哥: 哈哈哈哈哈哈哈!
@爱编程的大叔: 大叔为何如此狂笑
@爱编程的大叔: 问题我已解决,但还是感谢你的帮助











